Pontos de Lagrange: o que são e como resolveram um grande problema da física?

Pontos de Lagrange são lugares entre a órbita de dois corpos no espaço onde os campos gravitacionais de ambos se anulam. Eles são muito úteis para colocar telescópios, como é o caso do James Webb e o SOHO. Mas, além disso, eles ajudaram a resolver um dos grandes problemas da física.

• Como escolher seu primeiro telescópio doméstico?
• Como se tornar um astrônomo amador?

O problema dos três corpos

Prever a órbita de um planeta, asteroide, cometa ou estrelas é algo relativamente simples. Esses corpos costumam girar ao redor de algum outro objeto, como a Terra orbita o Sol e a Lua orbita a Terra. Sistemas binários de duas estrelas também se comportam de maneira semelhante, mas estão orbitando um ponto gravitacional em comum.

Na verdade, podemos descrever a órbita entre o Sol e a Terra da mesma forma — eles orbitam o mesmo centro gravitacional. O Sol também se move por causa do campo gravitacional do nosso planeta (e de todos os outros, mas vamos desconsiderá-los para analisar o sistema Sol-Terra).

Entretanto, a massa da Terra é tão pequena em relação à nossa estrela que o movimento solar ao redor desse ponto gravitacional é quase no centro gravitacional do próprio Sol. Ou seja, “dentro” dele. Por isso, desconsideramos esse movimento e dizemos simplesmente que a Terra orbita o Sol.

Mas estrelas binárias possuem massas consideráveis. Por isso, o centro gravitacional do sistema não está “dentro” de nenhum dos corpos. Ainda assim, é fácil prever as órbitas de ambas, usando a gravitação universal de Isaac Newton, que consiste em fórmulas bastante simples.

Entretanto, as coisas se complicam quando há três objetos ou mais orbitando o mesmo centro gravitacional. Esses sistemas são encontrados com certa facilidade em nossa própria galáxia, como os aglomerados globulares com centenas de estrelas gravitacionalmente ligadas entre si. Nesse caso, as estrelas podem ser simplesmente expulsas para longe (ou não).

A dificuldade de prever essas órbitas perturba os físicos desde os dias de Isaac Newton, porque três objetos orbitando entre si não seguem um caminho previsível definido por fórmulas matemáticas simples. Atualmente, cientistas usam modelos e simulações computacionais muito sofisticadas para lidar com o problema.

De acordo com a matemática, se os três objetos forem de tamanho e distância comparáveis em relação ao ponto central, uma “luta” pela prevalência ocorre, atirando o sistema no caos. Por isso, é impossível usar as fórmulas clássicas para prever as órbitas.

Havia uns pontos no meio do caminho

O problema de três corpos perturba matemáticos e físicos há 400 anos, mas há maneiras de lidar com ele de modo simples — pelo menos em alguns casos. Em 1722, o cientista suíço Leonhard Euler encontrou algumas soluções. Cerca de 50 anos depois, o ítalo-francês Joseph Louis Lagrange estendeu o trabalho de Euler.

Para isso, eles fizeram considerações simplificadoras: o problema se torna simples quando um dos objetos do sistema tem massa muito pequena em relação aos outros dois (de modo que sua gravidade poderia ser ignorada) e quando consideramos uma órbita bidimensional, ignorando outros movimentos. Nesse processo, descobriram "pontos neutros".

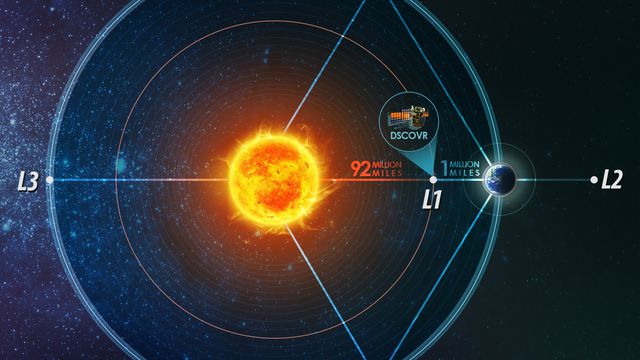
Os três primeiros pontos (L1, L2 e L3) ficam ao longo de uma linha que conecta as duas massas maiores. No caso do sistema Sol-Terra, por exemplo, L1 fica dentro da órbita da Terra, L2 fica fora dela e L3 fica no lado oposto do Sol. Neles, as forças gravitacionais do planeta e da estrela se anulam, desde que o objeto que estiver neles seja pequeno — como um satélite.

Já os pontos L4 e L5 estão localizados atrás e na frente da órbita do objeto de menor massa, formando um triângulo equilátero com os dois objetos. Lá, o efeito é o mesmo, com as forças gravitacionais se equilibrando igualmente. Um ótimo exemplo para visualizar os pontos L4 e L5 é o planeta Júpiter e os asteroides troianos, que estão à frente e atrás da trajetória do gigante gasoso.

Há algumas diferenças importantes, no entanto. Os pontos L1, L2 e L3 são instáveis, ou seja, a menor interferência mandará um satélite nesses locais para longe. Por outro lado, os L4 e L5 são estáveis e objetos neles tendem a permanecer por um longo período.

Todos os pares de objetos massivos tem seus cinco pontos Lagrange e, portanto, podem receber satélites e telescópios para funções estratégicas. Por exemplo, o L1 é um ótimo lugar para observar o Sol: ele pode ficar com uma câmera sempre apontado para nossa estrela e, do outro lado, com seu equipamento de comunicação sempre apontado para a Terra. Esse é o caso do Solar and Heliospheric Observatory (SOHO).

Já o L2 é um ótimo lugar para observar qualquer coisa, exceto o Sol, porque a estrela estará sempre parcialmente ocultada pela Terra, enquanto a comunicação permanece com as bases terrestres. Mesmo com o planeta entre o instrumento e o Sol, a energia solar ainda consegue fornecer energia. O Telescópio Espacial James Webb está neste ponto.

Fonte: Space.com